questionet
Backpropagation 요약 (sigmoid 함수와 tanh 함수의 미분) 본문
사용된 그래프 그림과 수식 이미지 출처는 다음과 같습니다
github.com/WegraLee/deep-learning-from-scratch-2
www.youtube.com/watch?v=dB-u77Y5a6A&list=PL5-TkQAfAZFbzxjBHtzdVCWE0Zbhomg7r&index=6
1. backpropagation
Deep Neural Network에서
경사하강법( W ← w - a*dL/dw )을 써서 optimization을 한다는 것은
모든 레이어의 각 노드에 있는 가중치들이 최종 Loss 값에 미치는 영향력을 알아냄으로써
손실함수의 결과값을 가장 작게 만드는 가중치 행렬을 구한다는 것이다.
이를 위해서는 각 가중치 w에 대해 최종 Loss값을 미분한 값을 구해야 한다.
backpropagation은
순전파를 통해 활성화 함수를 거쳐 나온 출력값이
최총 출력층에 도달하여 어떠한 scalar값을 갖게 되었을 때
이 최종 scalar 값을 시작으로 왔던 길을 되돌아가면서
각 노드의 출력값과 입력값을 바탕으로 계산한 미분 값을
역전파해 나가는 것을 의미한다.
이 순전파와 역전파를 반복하는 과정에서
최적의 가중치가 계속 업데이트 된다.
역전파시 개별 노드의 w에 대한 다음 레이어의 노드에서 온 기울기의 미분값은
체인룰(chain rule)을 사용하여 계산하는데
그 과정은 아래에 맨 처음 나오는 그림과 같다.
2. sigmoid 함수의 미분
DNN은 활성화 함수로 sigmoid, tanh, Relu등 다양한 함수를 사용한다.
아래 그림은 wx + b 가
활성화 함수로 쓰인 sigmoid 함수 f를 통과했을 때의 순전파와 역전파시 계산의 흐름을 나타낸 것이다.
x를 wx + b,
z를 x가 f를 통과한 후의 출력값이라고 하자.
우리가 구하고자 하는 downstream gradient는 local gradient와 upstream gradient의 곱셈(chian rule)으로 얻어진다.
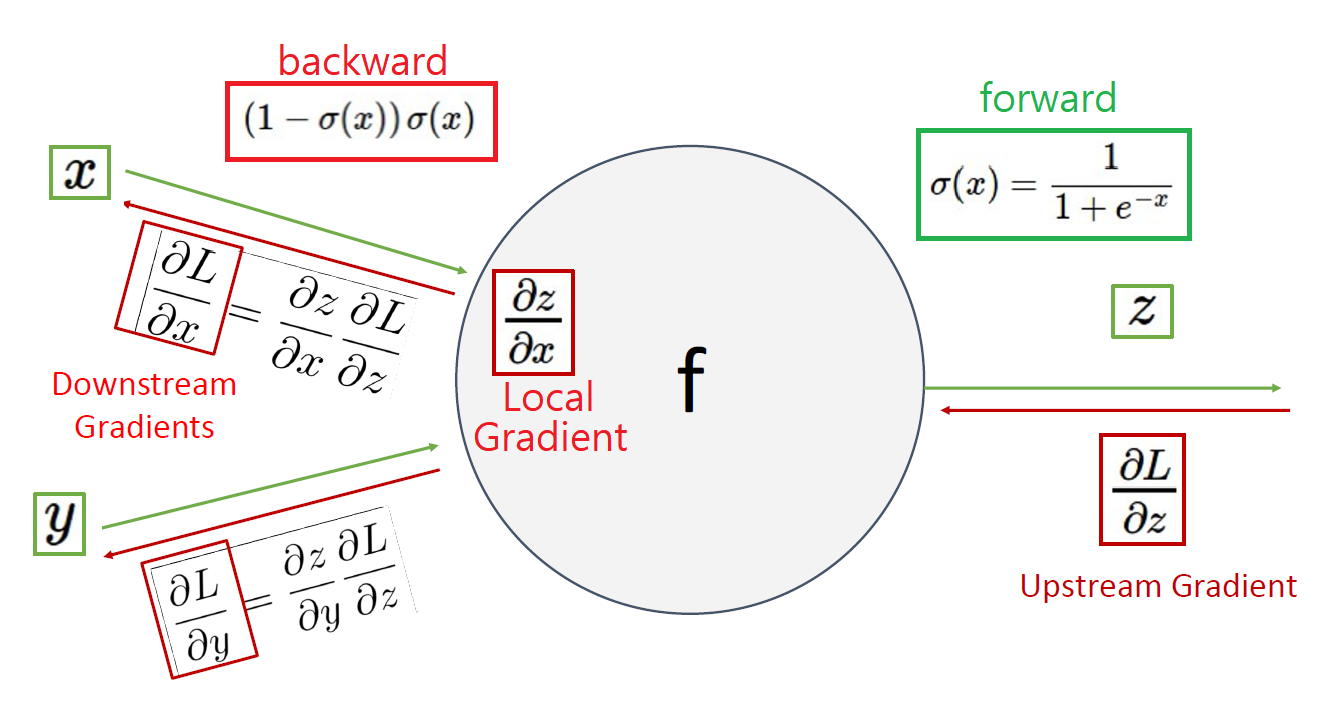
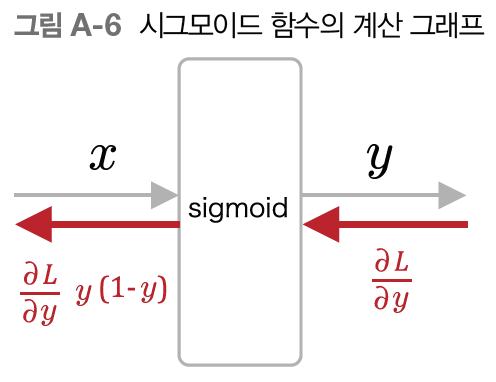
위 그래프의 local gradient 는 (1-σ(x))·σ(x),
즉 아래 그래프의 y·(1-y) 이다.
이 값이 어떻게 계산된 것인지 살펴보자.
시그모이드 함수는 다음과 같다.
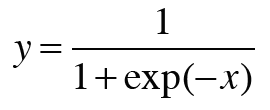
해석적 미분으로 바로 구해도 되지만, computaional graph로 구하면 다음과 같다.
※ 계산 그래프로 미분 값을 구하는 과정은
해석적 미분을 했을 때보다 이해하기 쉽다는 장점도
역전파 메커니즘을 이해하는 데도 도움이 된다.
계산 그래프는 수식의 각 연산을 노드로 간주해 입력값과 출력값을 나타낸 것이다.

시그모이드 함수의 분모를 x로 치환했을 때,
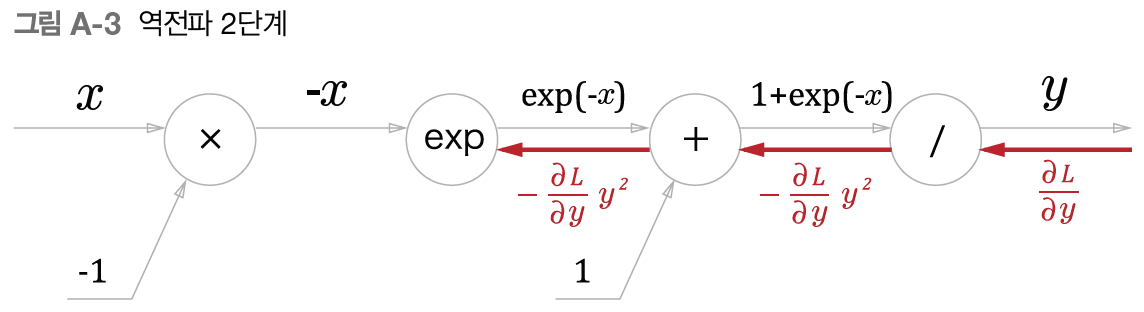
x에 대한 y의 미분 값을 구하는 과정은 다음과 같다.

나누기 연산 노드에서 local gradient는 마이너스 y제곱 임이 위의 계산결과를 통해 도출되었으므로
upstream gradient인 dL/dy 와 곱한 값 downstream gradient를 이전 노드로 흘려보내준다.
그런데 이전 노드는 + 연산 노드이므로
그대로 통과해 exponential 연산 노드로 보내준다.
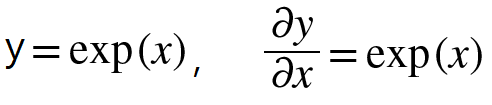
자연상수 e의 지수함수 e**x를 미분한 값은 자기자신이 된다.
따라서 exp 노드에서 local gradient는 순전파시 출력값이었던 e**-x 가 되므로
upstream gradient와 곱하여 이전 노드로 보내준다

마지막 곱하기 노드에서는 mul gate 에 따라 upstream gradient에 마이너스를 곱한 값이
downstream gradient가 되고,
최종 값은 아래와 같이 정리할 수 있다.
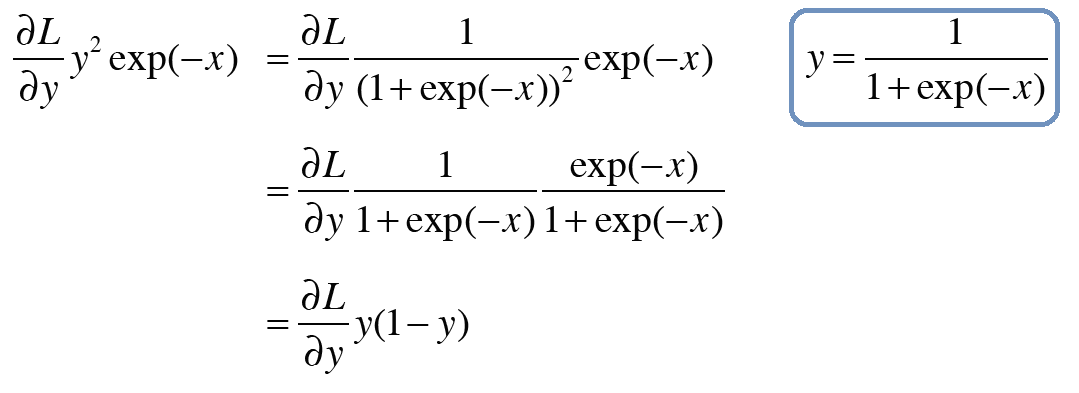
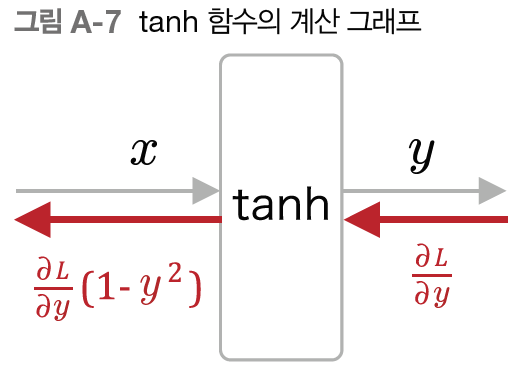
이제 아래 그래프의 의미를 이해할 수 있다.
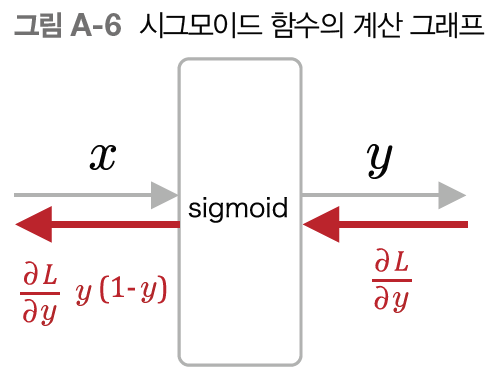
3. tanh 함수의 미분
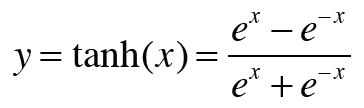
활성화 함수로 tanh함수를 썼을 경우 우리가 구해야 하는 것은 다음과 같다.
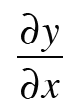
tanh 함수를 미분하기 위해 두 개의 식을 사용한다
1. 몫의 미분 공식이 필요하다. (f(x)/g(x)의 미분)
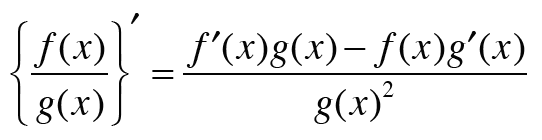
※몫의 미분 공식은 곱의 미분 공식으로 유도할 수 있다.
{f(x)g(x)}' = f'(x)g(x) + f(x)g'(x)
2. 네이피어수(자연상수) e의 미분값도 필요하다
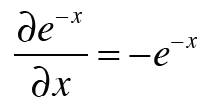
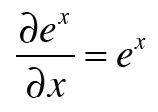
위의 식들을 사용해 아래와 같이 구할 수 있다.
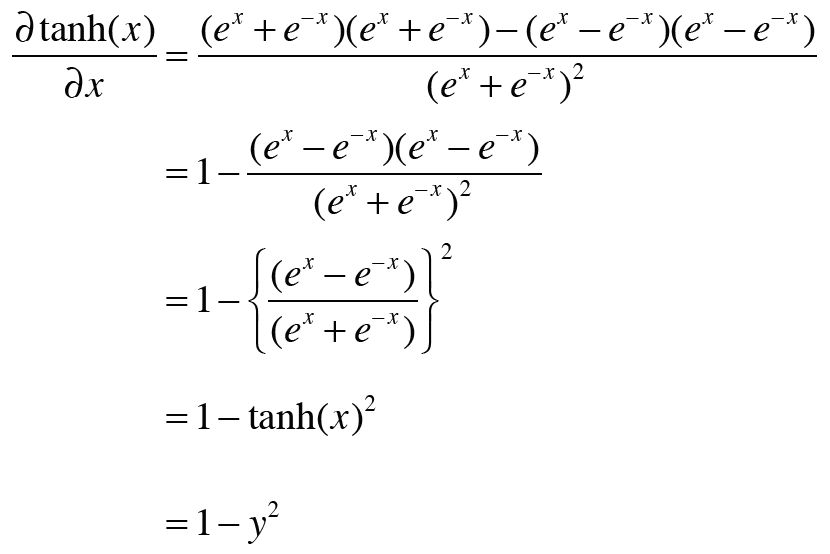
'Deep learning > 딥러닝 학습기법' 카테고리의 다른 글
| delve into LoRA # 로라 파헤치기 (1) (0) | 2023.11.11 |
|---|---|
| word2vec (0) | 2021.02.08 |
| Backpropagation 설명 (역전파) (0) | 2021.01.31 |
| 신경망 학습 (경사하강법) (0) | 2021.01.22 |
| Optimization (최적화 기법) (0) | 2021.01.17 |



