questionet
Backpropagation 설명 (역전파) 본문
이 페이지는 다음 강의 영상을 정리한 것이다.
www.youtube.com/watch?v=dB-u77Y5a6A&list=PL5-TkQAfAZFbzxjBHtzdVCWE0Zbhomg7r&index=6
살펴볼 주제
1. computational graph로 backpropagation을 계산했을 때 발견되는 pattern의 의미와 그 쓰임
2. input과 output이 scalar가 아닌 vector 또는 tensor일 때 backpropagation이 진행되는 구체적인 과정

computational graph를 통해 backpropagation 을 계산할 때
미분 값이 역전파 되어가는 데 있어 몇 가지 pattern 을 발견할 수 있다
1. add gate : gradient distributor
node 연산이 더하기일 경우 ( 덧셈 연산을 수행하는 함수를 미분할 경우) 미분 값(local gradient)은 1이 된다
이때는 downstream gradient가 upstream gradient x 1 이 되므로
f(x, y) = x + y,
df(x, y)/dx = 1 , df(x, y)/dy = 1
downstream gradient는 upstream gradient와 같은 값이 된다. (즉 gradient가 그대로 propagate 된다)
그래서 add node를 단순한 gradient distributor로 간주할 수 있다.
2. copy gate : gradient adder
input이 하나고 output은 두 개를 갖는 노드인 경우
각각의 upstream gradient 단순히 더해주면 된다.
이런 형태의 노드는 weight regularization 에서 볼 수 있다.

* add gate의 input, output 값을 forward pass 관점에서 보면 copy gated의 역전파와 같고
copy gate의 input, output값을 forward pass 관점에서 보면 add gate의 역전파와 같다.
3. mul gate : swap multiplier
곱하기 노드의 경우, downstream gradient는 upstream gradient 에 input값을 서로 바꾸어 곱한 값과 같다.
f(x, y) = xy,
df(x, y)/dx = y , df(x, y)/dy = x
왜냐하면 각 input의 local gradient는 상대의 input값과 같기 때문이다.
Q1 : 강의에선 mul gate 는 forward pass 일 때와 backward pass 일 때 모두 곱하기 연산이 일어나서
mul gate를 많이 갖고 있는 모델일 때, 문제가 될 수 있는 모델이 있을 수 있다고 하는 데,
어떤 모델이, 왜 문제가 되는걸까?
4. max gate : gradient router
input 값 중 더 큰 값을 취하는 노드의 경우, cf) Relu함수
backpropatation을 하면 input이 더 컸던 쪽은 upstream gradient를 그대로 받게 되고
input이 더 작았던 쪽은 gradient가 0이 된다.
(max함수의 정의에 따라 더 큰 값만 의미가 있고 작은 값은 아무 역할도 하지 못하므로)
Q2 : 강의에선 max gate를 많이 갖고 있는 모델은, backpropagation을 할 때 gradient가 0이 되는 경우가 많아지므로
good gradient flow 를 얻기가 어려워지는 문제가 생겨 max gate를 선호하지는 않게 된다고 한다.
분명히 이해가 되지는 않는데, 이것이 leaky Relu와 관련이 있는걸까?
computational graph로 backpropagation을 실행한 과정을 code로 구현하는 두 가지 방식
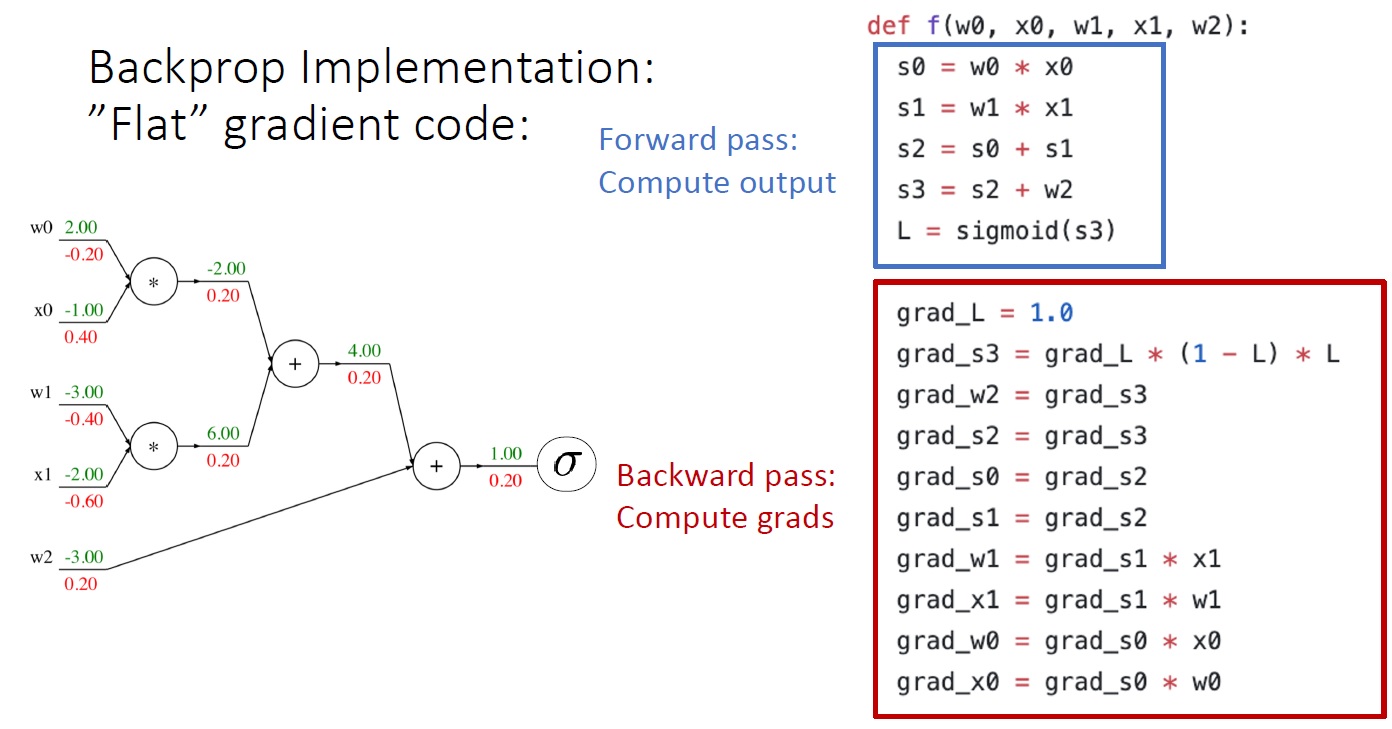
1. 'flat' gradient code
위의 코드들은 파이썬 언어로 작성한 것인데,
backward pass 코드들이 forward pass 코드의 순서를 거꾸로 되짚어 가며 만든 형태를 띤다.
backpropagation을 코딩하는 건
위에서 살펴본 backpropagation gate pattern 들을
forward pass의 역방향으로 순서에 맞춰 쓰기만 하면 되는 걸 알 수 있다.
그래서 이런 방식의 backpropagation coding을 강의에선 'flat' 한 backpropagation code 라고 부르고
이런 방식의 코딩에 먼저 충분히 익숙해 질 것을 권유한다. (기초를 다지는 의미에서)
그런데 flat gradient coding은
모델을 바꾼다거나 활성화 함수, loss function 또는 rerularization term을 다른 걸 쓰면
바뀐 모델의 형태나 식에 맞춰 코드를 전부 다시 써야 한다.
2. Modular API
좀더 모듈러한 방식으로 코딩을 한다면 아래와 같이 할 수 있다.

위 코드는input 과 output이 scalar 라고 가정한 mul node(gate)를 파이토치로 구현한 것이다.
이 코드가 flat version 보다 좀 더 modular 한 까닭은
node 단위로 코딩을 한 점,
클래스를 써서 forward pass 부분과 backward pass부분을 메소드로 처리한 점,
forward 함수의 코드블럭을 보면 입력으로 받은 x, y를 local gradient로 쓰기 위해 미리 저장해 두는 코드를 쓴 점 등
flat version에서 모든걸 하나의 함수에 넣은 것과 비교해
훨씬 수정이 용이하고 갖다 붙여 쓰기 편하다는 데 있다.
* pytorch github repo에 들어가보면 위와 같은 모듈 코드들이 많이 있으니 참고.
github.com/pytorch/pytorch/tree/master/aten/src
지금까진 input과 output이 scalar일 때의 backpropagation 과정을 살펴보았다.
그럼 이제 실전에서와 같이
input, output이 vector, tensor 형태일 때의 backpropagation은 어떻게 실행되는지 살펴보자.

input은 n차원 vector이고 output은 scalar일 때,
downstream gradient는 input과 같은 n차원 vector 형태가 될 것이다.
좀 더 일반화 해서
input이 n차원 vector, output이 m차원 vector 라면
downstream gradient는 n by m 형태의 matrix가 될 것이다. (이러한 행렬을 Jacobian 자코비언 행렬이라고 부른다)
Q3. 이게 무슨 뜻일까?
*Jacobian matrix 참고
angeloyeo.github.io/2020/07/24/Jacobian.html
computational graph를 통해 backpropagation을 이해하는 방법의 장점은
single node 단위에서 backpropagation이 어떻게 진행되는지 따져보기만 하면 된다는 데 있으므로
이제 input과 output이 모두 벡터인 경우는 어떻게 되는지 아래 그림을 통해 살펴보자.

여기서 input은 각각 x, y 두 벡터이고 (Dx, Dy로 표기) output은 역시 vector인 z이다. (Dz로 표기)
*여기서 z가 vecotor라고 해서, loss가 vector 형태일 거라고 생각해선 안된다.
*최종 loss값은 항상 scalar다.
따라서 upstream gradient인 dL/dz의 의미는
이 node의 output인 z의 각 원소들이 아주 미세하게 변할 때, scalar값인 loss가 어떻게 변하는 지를 의미한다.
*좀 더 수학적으로 말하면 dL/dz 벡터는 loss값을 z로 편미분한 벡터다.
dz/dx 의 의미는 이 node에서 함수 f에 대해 입력 벡터 x의 각 원소들이 미세하게 변할 때
출력 벡터 z의 각 원소들이 얼마나 변하는 지를 편미분한 local gradient이다.
그런데 함수 f는 여러 개의 변수 (여기서는 x, y)를 가진 다변수 벡터함수(vector valued function) 이다.
* 여기서 벡터함수는 벡터를 입력 받아 벡터를 출력하는 함수를 의미하는 함수로 쓰였다
여기서 잠시 vector valued function와 자코비언 행렬이 backpropagation에서 무슨 의미를 지니는 것인지 살펴보자

Q3의 답 : 예를 들면 위 그림에서 함수f는 변수 두 개(x, y)를 입력으로 받아 출력을 3개로 내놓는 다변수 벡터함수다.
이 함수f의 도함수f'를 구하려면 각 함수 f1, f2, f3에 대해 편미분을 해야 한다.

변수가 x, y두 개 이므로 두 변수에 x, x + y, xy를 각각 편미분을 하면
오른쪽과 그림과 같이 2 by 3 행렬이 된다. 이 행렬이 함수 f의 자코비언 행렬이다.
즉 자코비언 행렬이란 편미분할 변수가 많고, 그 변수들로 이루어진 함수도 많을 때
각 변수에 대한 각 함수의 편미분 값을 원소로 갖는 행렬이다.
다시 말해 n개의 변수를 가진 함수가 m개 있다면 그 함수의 자코비언 행렬은 n by m 형태를 띤다.
다시 위 노드로 돌아가면,
따라서 이 local gradient dz/dx는
x가 n차원 벡터, z가 m차원 벡터인 경우 n by m 형태의 jacobian matrix 형태가 된다.
정리하면, 이 node에서 local gradients는 jacobian matrix 의 각 원소가 된다.
결과적으로 우리는 x, y, z의 값을 알기 때문에
x와 y의 local gradient 값을 바로 계산할 수 있고
dz/dx , dz/dy
upstream gradient인 dL/dz가 주어졌으므로 chain rule을 써서
downstream gradient인 dL/dx와 dL/dy를 구할 수 있다.
dL/dx = dz/dx * dL/dz
dL/dy = dz/dy * dL/dz
이 때 dz/dx, dz/dy는 자코비언 행렬이고, dL/dz는 벡터이므로
최종적으로 우리가 구하고자 하는 dL/dx, dL/dy는 행렬-벡터 곱 (matrix vector product) 연산이 된다.
중요한 것은 이 matrix-vector multiplication 의 결과가 입력 벡터 x, y 의 shape과 똑같다는 것이다.
이제 구체적인 사례를 통해 vector를 edge로 갖는 node의 backpropagation 과정을 살펴보자.
예를 들어 우리의 모델에 아래와 같은 노드가 있다고 하자.

여기서 함수f는 vector valued Relu function이라고 볼 수 있다.
(입력 벡터의 원소 중 0보다 큰 값만 그대로 출력 벡터의 원소가 되게 하고, 0보다 작은 원소는 0이 되게 하는)
이제 upstream gradient가 위와 같이 주어졌을 때
(Relu function의 output vector 값들이 아주 조금 변했을 때 최종 loss 값이 얼마나 변하는 지의 비율)
맨 처음 살펴본 backpropagation pattern 들 중 하나인 max gate에 따라
dy/dx 는 위와 같은 형태의 행렬이 된다
(여기서 jacobian matrix dy/dx의 의미는 input값의 변화에 따라 output값이 변하는 정도를 나타내는 비율을 의미한다)
여기에 upstream gradient dL/dy 를 곱해주면, downstream gradient dL/dx를 얻을 수 있다.
활성화 함수로 Relu function을 쓴 경우, 그 노드의 backpropagation을 위한 Jacobian matrix는
그림과 같이 일종의 대각선 행렬과 같은 형태가 되는데,
대각선을 제외한 모든 원소들은 0이 되는 'sparse'한 특징을 보인다.
input vector의 차원수가 n이라면 , Jacobian matrix의 shape는 n제곱만큼 늘어난다.
일반적으로 neural network에서 처음에 입력받는 feature값은 최소 수백개이므로
자코비언 행렬도 엄청나게 커지지만 무엇보다 그 행렬의 원소들 중 거의 대부분이 0이라는 게
컴퓨터 연산자원 활용에 있어 아주 큰 비효율을 낳게 된다.
그래서 자코비언 행렬을 있는 그대로(explicitly form) 쓰지 않고
implicit하게 사용하는데 그 방법은
그냥 upstream gradient vector를 max function(Relu function?)에 넣어버리는 것이다.
즉 Relu함수를 쓴 node의 backpropagation은 foward pass때와 마찬가지로 max function을 gate로 쓰는 것이다.
여기서 중요한 것은 upstream gradient 값 중에서 0보다 큰 값을 선별하는 기준으로 x input vector를 쓴다는 점이다
이제 마지막으로 matrix 또는 tensor를 를 edge로 갖는 node의 backpropagation을 살펴보자.

tensor란 vector와 matrix를 일반화한 것을 뜻한다.
(예컨대 한 image의 경우 가로, 세로 pixel의 개수와 RGB 3 channel 총 3개의 차원을 가지므로 3차원 텐서라 할 수 있다)
위의 그림의 경우 입력값 x, y와 출력값 z는 matrix 형태다.
upstream gradient는 y와 r같은 형태의 행렬로 주어진다.
여기서 자코비언 행렬은 [(Dx * Mx) * (Dz * Mz)] 처럼 very high rank tensor가 된다.

dL / dx를 또는 dL/dw를 어떻게 구하면 좋을까?
원소별로 접근해본다.

dy(1,1) / dx(1,1) 를 구하기 위해선
x(1,1)w(1,1) + x(1,2)w(2,1) + x(1,3)w(3.1) 을 x(1,1)에 대해 편미분 해주면 된다.
그 값은 w(1,1)과 같다.
이러한 방법으로 dy/d(x1,1)을 모두 구하면

y 는 2 x 4 행렬이므로
1행은 w(1,:)과 같고 2행은 모두 0이 되는 2 x 4 행렬을 얻을 수 있다.
*2행이 모두 0이 되는 이유는 x(1,1)에 대해서 편미분을 하는 중이므로
2행의 원소값에는 x(1,1)이 들어 있지 않아 모두 상수처리 되기 때문이다.
이제 chain rule을 적용해 dy/dx(1,1) X (dL/dy)를 하면
dL/dx(1,1)은 W(1,:) 과 dL/dy(1,:)를 element-wise product해 모두 더한 값과 같게 된다.
처음에 여기서 dy/dx(1,1)과 (dL/dy)은 똑같이 2 x 4 행렬인데 어떻게 곱셈을 할 수 있느냐는 함정에 빠졌는데
dy/dx(1,1)은 위 [(2 x 3) x (2 x 4)] 자코비언 행렬에서 x(1,1)에 해당하는 행렬을 떼어낸 것이므로
2차원이 아니라 3차원적인 관점에서 봤을 때, 평면에 놓인 좌우 두 행렬의 곱이 아닌
3차원 공간에 놓인 앞뒤 행렬의 같은 위치에 놓인 원소별 곱으로 보면 이해가 됐다.
아마 이것이 matrix backpropagation을 할 때 자코비언 행렬이 very high rank tensor로 불리는 까닭인 것 같다.
만약 내 해석이 맞다면, 2차원 matrix 가 아니라 3차원 배열, 다차원 배열로서의 tensor가 input으로 주어질 때
자코비언 행렬은 도저히 상상이 안된다.
그렇다면 이러한 복잡한 연산과정이 Q1에 대한 한 가지 답변이 될 수 있을까?
이 연산을 dL/dx(i,j)에 일반화하면 downstream gradient는 아래와 같은 form으로 구할 수 있다.

x에 대한 downstream gradient는 upstream gradient 곱하기 w의 전치행렬이 되고
w에 대한 downstream gradient는 x의 전치행렬 곱하기 upstream gradient가 된다.
행렬곱 연산을 위해 reshape해준 걸 차치하면
곱하기 노드를 backpropagation 할 때 보게 되는 mul gate와 유사한 pattern을 가진다.
'Deep learning > 딥러닝 학습기법' 카테고리의 다른 글
| delve into LoRA # 로라 파헤치기 (1) (0) | 2023.11.11 |
|---|---|
| word2vec (0) | 2021.02.08 |
| Backpropagation 요약 (sigmoid 함수와 tanh 함수의 미분) (2) | 2021.02.02 |
| 신경망 학습 (경사하강법) (0) | 2021.01.22 |
| Optimization (최적화 기법) (0) | 2021.01.17 |




