비선형 자료구조 : 그래프(graph)

그래프란?

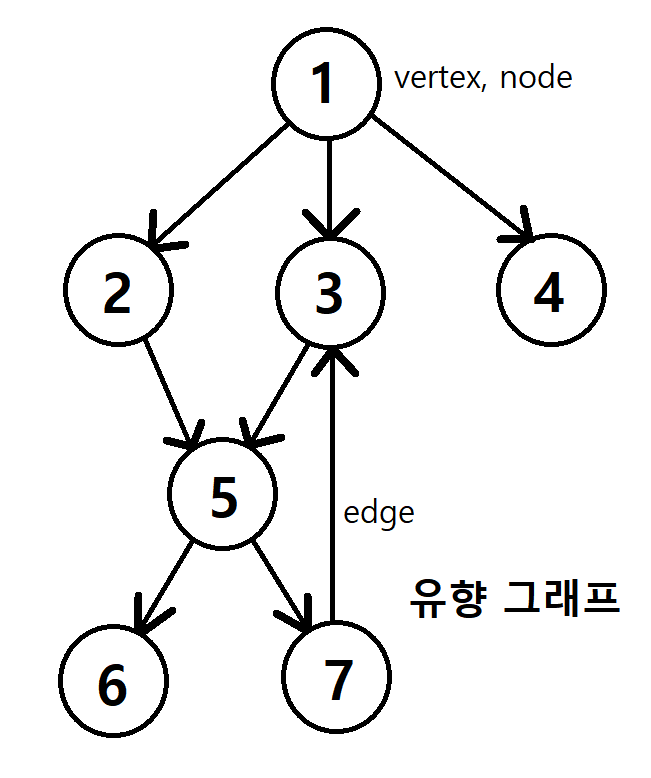
그래프는 정점 · 꼭지점(vertex)과 간선 · 변(edge)으로 구성된 자료구조를 의미한다.

그래프를 구현하는 방법

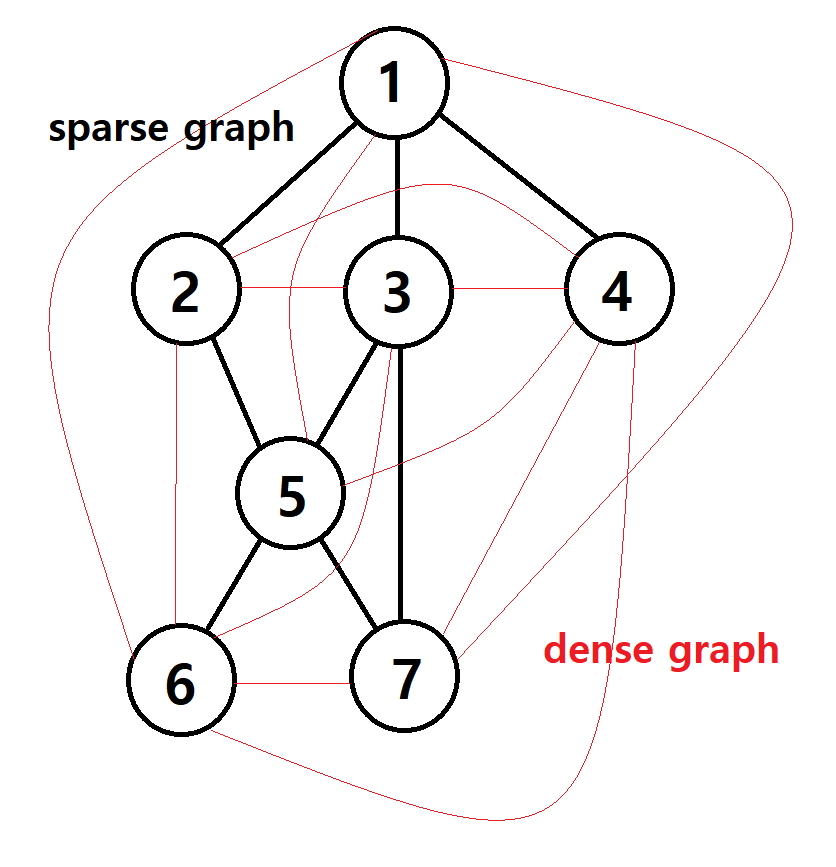
그래프를 표현하는 방법에는 인접리스트(adjacency list)와 인접행렬(adjacency matrix)이 있다.

인접리스트로 표현한다는 건 무슨 말일까?    각 노드가 인접한 노드의 리스트를 가지고 있는 구조다.   파이썬에서는 딕셔너리 자료형을 사용하면   출발 노드를 key로 도착노드를 value로 표현할 수 있다.   도착노드는 여러 개가 될 수 있으므로 리스트 형태가 된다.   graph = { 1 : [2, 3, 4,],                2 : [5],                3 : [5],                4 : [ ],                5 : [6, 7],                6 : [ ],                7 : [3],             }

 

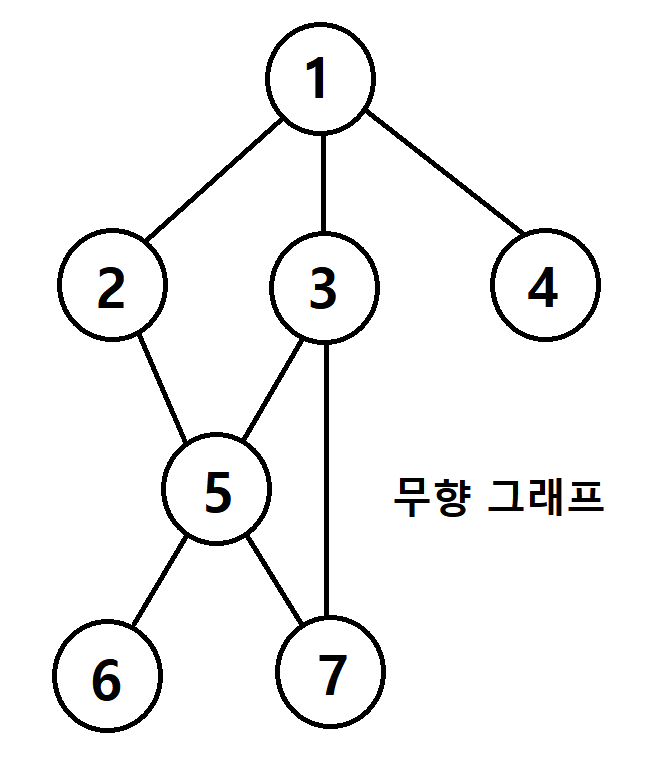
리스트 구조는 sparse graph에 적합하며    적은 메모리 공간을 요구한다.   행렬 구조는 많은 양의 메모리를 필요로하지만   더욱 빠른 접근을 제공한다. (dense graph에 사용)   실제 적용에 있어서 최적의 자료구조는   이 두 구조의 조합된 형태를 띤다	방향성을 가지지 않은 그래프에서는   불필요한 정보가 생긴다.   예를 들어 만약 ③과 ⑤가 인접하다면   ③의 인접 리스트는 ⑤를 포함하게 되며   동시에 ⑤의 리스트에도 ③이 포함된다.   추가적인 저장 공간에 대한 비용이 있다면   인접 정보를 얻는 것은 빨라진다.

 

트리와 그래프의 차이

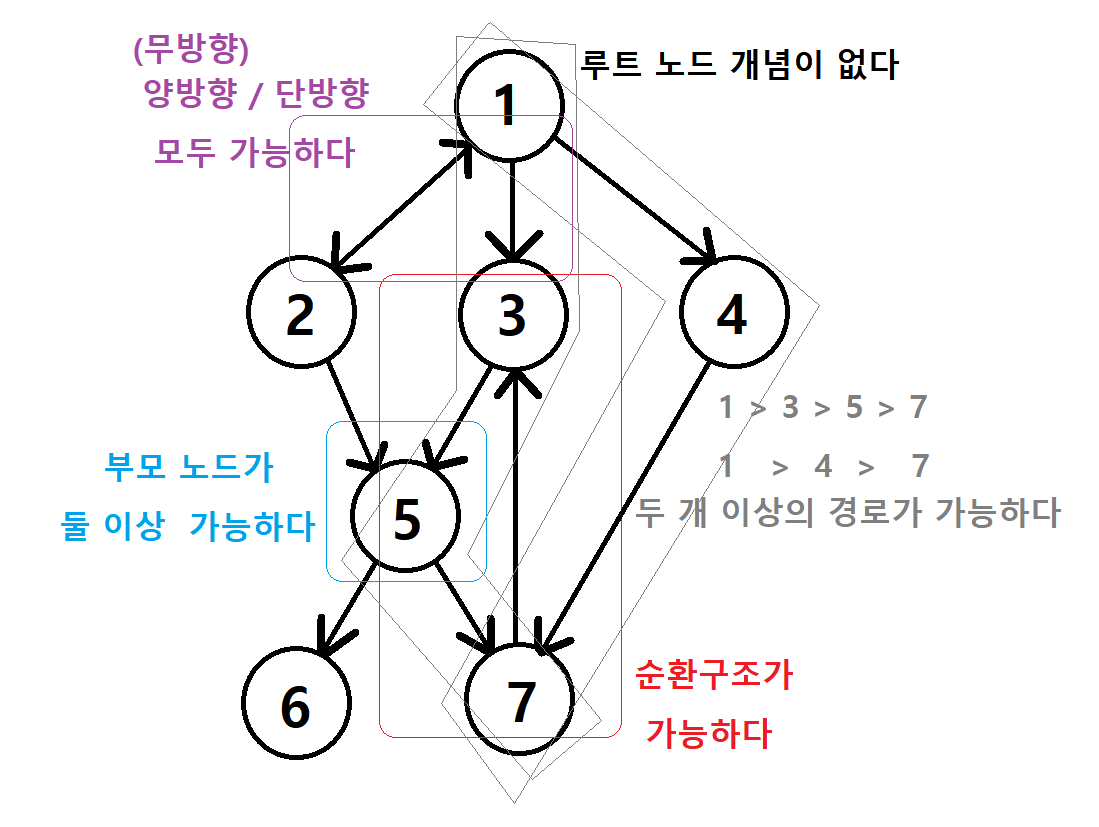
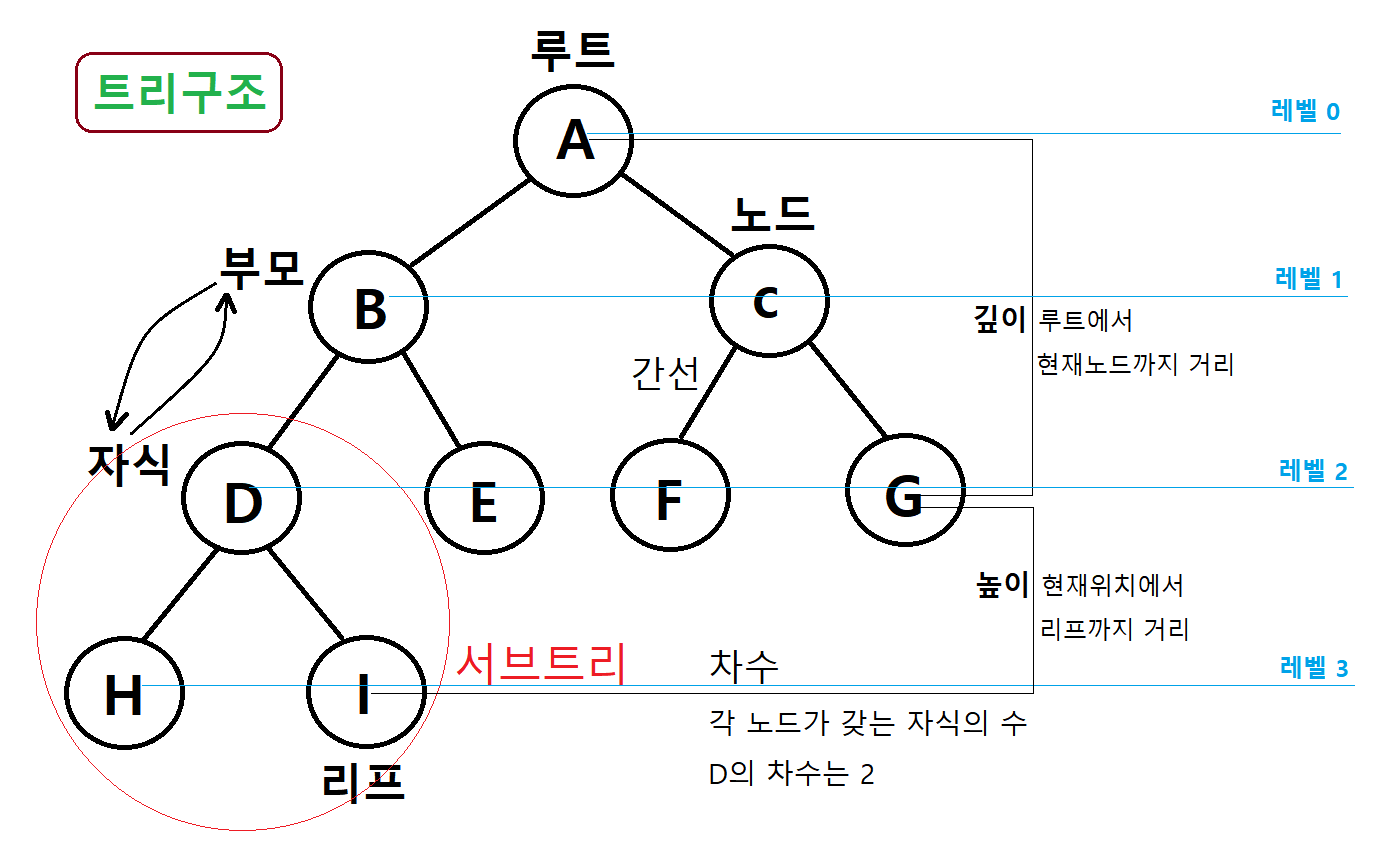
트리는 특수한 형태의 그래프다

1. 단방향이다 (순환 구조가 없다)
   
2. 하나의 부모 노드를 갖는다

3. 루트는 하나여야 한다

그래프 순회 (그래프 탐색 search)

그래프의 각 정점을 방문하는 과정을 말한다.

깊이우선탐색과  너비우선탐색이 있다. 

깊이 우선 탐색 : depth first search (이하 DFS)  1. 주로 스택으로 구현하거나 재귀로 구현한다. 2. 너비우선탐색에 비해 널리 쓰인다.(코테에서도)

너비 우선 탐색 : breadth first search (이하 BFS) 1. 주로 큐로 구현하며 (재귀를 사용할 수 없다) 2. 그래프의 최단 경로 문제를 풀 때 사용된다.

 

 

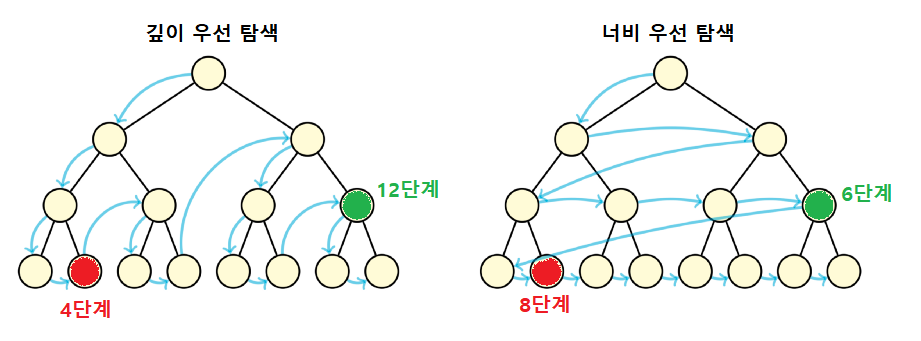
깊이 우선 탐색의 세 가지 스캔 종류

백트래킹 backtracking
백트래킹은 탐색을 하다가 더 이상 갈 수 없으면 왔던 길을 되돌아가 다른 길을 찾는 방법이다.
DFS와 같은데 DFS보다 광의의 의미를 지닌다.
주로 재귀로 구현하며 제약충족문제 constraint satisfaction problem (CSP)를 푸는데 필수적인 알고리즘이다.

그래프 구조, 그래프 순회(백트래킹)의 현실적 의미

미로에서 출구 찾기 문제

갈림길과 막다른 곳(제약)이 있는 미로에서 나가는 방법(해)를 찾는 문제는 제약충족문제다.

방법1. 통로를 따라 걸어가다가 나가는 길을 찾을 때까지 갈림길에서 아무쪽으로나 가라

이 방법은 쥐가 미로에서 길을 찾는 방법이다. 무작위로 이곳저곳을 기어가기 때문에
random mouse 방법이라고 부른다. 이 방법은 시간이 많이 걸린다

방법2. 벽에 오른손(왼손)을 대고 벽을 따라가다가 갈림길이 나오면 오른쪽(왼쪽)으로만 가라 

이 방법은 나가는 길을 결국 찾을 수 있다. 어떻게 이 방법이 효과가 있는 걸까?
미로를 사실상 직선으로 만들 수 있기 때문이다.  그러니까 미로를 하나의 끈으로 만든다.

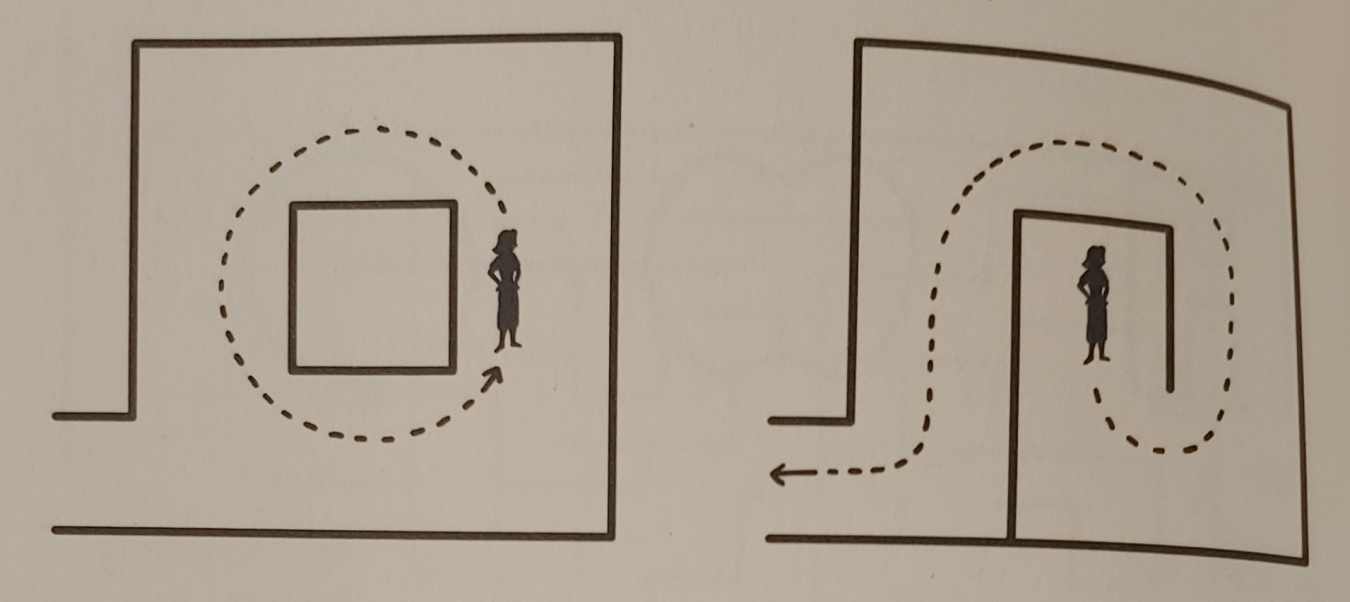
끈 한쪽을 따라가면 결국 다른쪽 끝에 도달하게 된다. 오른손법 또는 왼손법이라고 부른다.
이 방법은 오래 걸릴 순 있지만 방법1보다는 빠르게 나갈 수 있다.
단 미로 내부에 섬이 있는 경우에는 전혀 효과가 없다.
섬이란 손을 대고 있는 벽면과 연결되지 않는 미로 내부의 고리 모양으로 이어진 또 다른 벽면이 있는 구조를 말한다
만약 섬에 손을 얹어서 시작했다면 영원히 섬을 돌게 될 것이다. 

방법3. 미로를 걷는 동안 계속 실타래를 풀어라. 만약 막다른 곳에 다다르거나
          실에 발이 걸리면, 직전에 왔던 갈림길로 돌아가서 다른 방향으로 가라

이 방법을 역추적backtracking 이라고 부른다. 
이 방법은 막다른 곳에 도달할 때마다 온길을 되짚어 나가 다른 길을 찾을 수 있다. 
이 전략의 기원은 트레모의 알고리즘이라고 한다. (트레모라는 사람이 1882년 미로탈출 문제를 풀다가 만든게 DFS라고 한다)
갈림길의 교차로마다 표시를 하는 방법도 비슷한 방법이다.
이 방법은 방법1보다 빠르면서 섬이 있어도 탈출할 수 있다. 
(미로를 새로운 미로(하나의 끈)으로 만드는 것과 같다)

이 세가지 방법이 최단경로는 아니다. 다른 방법들도 있다.
(최단경로로 탈출하는 것도 중요하지만  지금 여기서 더 중요한 것은 '미로를 탈출한다'는 것이다.

즉 여기서 핵심은 미로처럼 제한된 환경에서 한 지점에서 다른 지점으로 이동한다는 개념이다.
(끈의 한쪽 끝에서 다른 쪽 끝으로 이동하는 것)
이것은 그래프 구조 (네트워크 구조라고도 한다) 를 탐색하는 일과 같다.
그래프의 edge선이 미로의 통로에 해당하고 정점vertex(꼭지점)이 미로의 갈림길에 해당한다.

미로 탈출과 네트워크의 유사성을 알아봤다.
이것이 어떤 현실의 문제 해결에 적용될 수 있을까? 

1 도로가 어떻게 연결돼 있는지 아는 지도 어플리케이션은 집에서 바닷가까지 가는 최상의 길을 알려준다. 

2 잘 만든 로봇청소기는 무작위로 돌아다니지 않고 먼저 방의 지도를 그려서
  벽과 구석과 모서리가 어디에 있는지 알아두고 난 다음,
  한쪽 끝에서 다른 쪽 끝으로 격자 같은 패턴을 그리며 이동할 것이다.

3 사람, 장소 ,사물이 어떻게 연결되어 있는지 아는 검색알고리즘은 더 나은 검색 결과를 제공한다

4 미로의 갈림길들은 명제에 해당하며 막다른 길에 다다른 것은 논증이 타당하지 않음을 뜻하고
  출구를 찾은 것은 논증의 결론이 그 전제들로부터 논리적으로 도출된다는 뜻이다.

5 그럼 출구가 존재하는 미로에서 모든 반론을 찾는다는 건(모든 막다른 곳을 찾는다는 건) 나쁘기만 한 걸까?
  cf) 다윈은 진화론을 발표하기 전 20년 가까운 시간을 가능한 반론을 모두 찾는데 소비했다.

그래프의 종류

1. 무방향(양방향) 그래프
   방향 그래프

2. 가중치 그래프 (Edge에 비용(통신망의 사용료)이나 가중치(회로)가 할당된 그래프, 네트워크라고도 한다)

3. 연결 그래프 (모든 정점 쌍들에 대해서 경로가 존재하는 그래프)
   비연결 그래프 (특정 정점쌍 사이에 경로가 없는 그래프)  위 미로 탈출 문제를 예로 들면 섬이 비연결 그래프에 해당

4. 순환 그래프
   비순환 그래프

5. 완전 그래프 (모든 정점 쌍들이 서로 연결된 그래프) dense graph에서 밀도가 1인 그래프가 완전 그래프에 해당

 

그래프 구조의 역사

1. 오일러 경로 - 쾨니히스베르크 다리 (1735년 오일러가 이 문제를 풀었다고 한다)

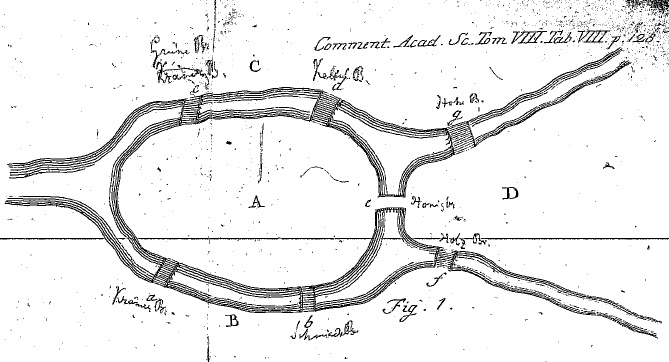
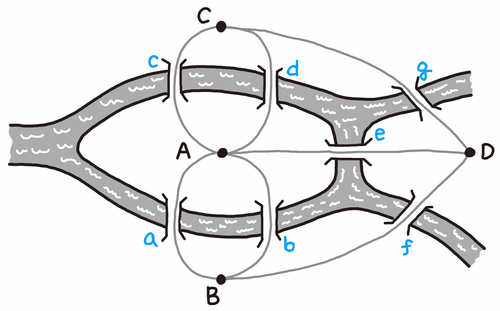
"모든 정점이 짝수 개의 차수를 가지면, 모든 다리를 한 번씩만 건너서 도달하는 게 가능하다."

(여기서 다리는 edge 간선에 해당한다. 
따라서 모든 간선을 한 번씩 방문한다는 말이 된다.
이러한 그래프를 '오일러 경로'라고 한다.
어떤 그래프가 오일러 경로라는 것은 한붓 그리기가 가능하다는 말과 같다)

2. 해밀턴 경로
각 정점을 한 번씩만 방문하는 무향 또는 유향 그래프를 
해밀턴 경로라고 한다.

오일러 경로는 Edge를 기준으로 하고, 해밀턴 경로는 Vertex를 기준으로 한다.

3. 외판원 문제
각 도시를 방문하고 돌아오는 가장 짧은 경로를 찾는 문제

각 정점을 한 번씩만 방문하고 출발지로 돌아오는 경로를 해밀턴 순환이라고 한다.
따라서 외판원 문제는 최단거리의 해밀턴 순환을 찾는 문제다.

해밀턴 경로는 NP-완전문제, 외판원 문제는 NP-난해문제 라고 불리며 
P-NP 문제와 함께 컴퓨터 과학 분야에서 중요한 문제라고 한다.